二叉排序树

介绍

二叉排序树又称二叉搜索树，听名字都知道是方便排序和查找的树

定义

可以是一颗空树 或者是具有如下性质的二叉树

• 若左子树不空 则左子树上所有节点的值都小于根节点的值
• 若右子树不空 则右子树上所有节点的值都大于根节点的值
• 它的左右子树也都是二叉排序树

特点

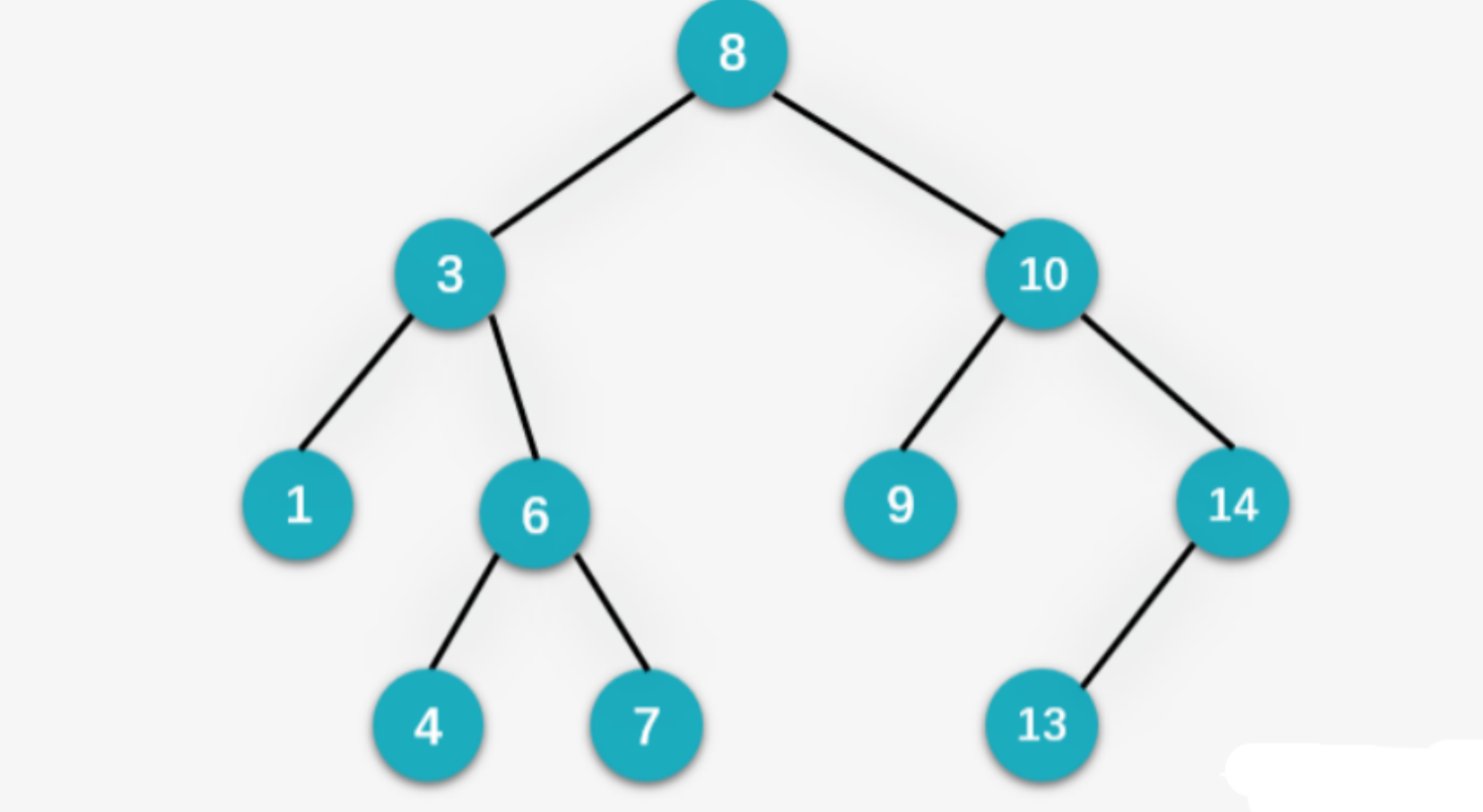
中序遍历是一个有序序列，比如上图的中序遍历结果是: [1, 3, 4, 6, 7, 8, 9, 10, 13, 14]

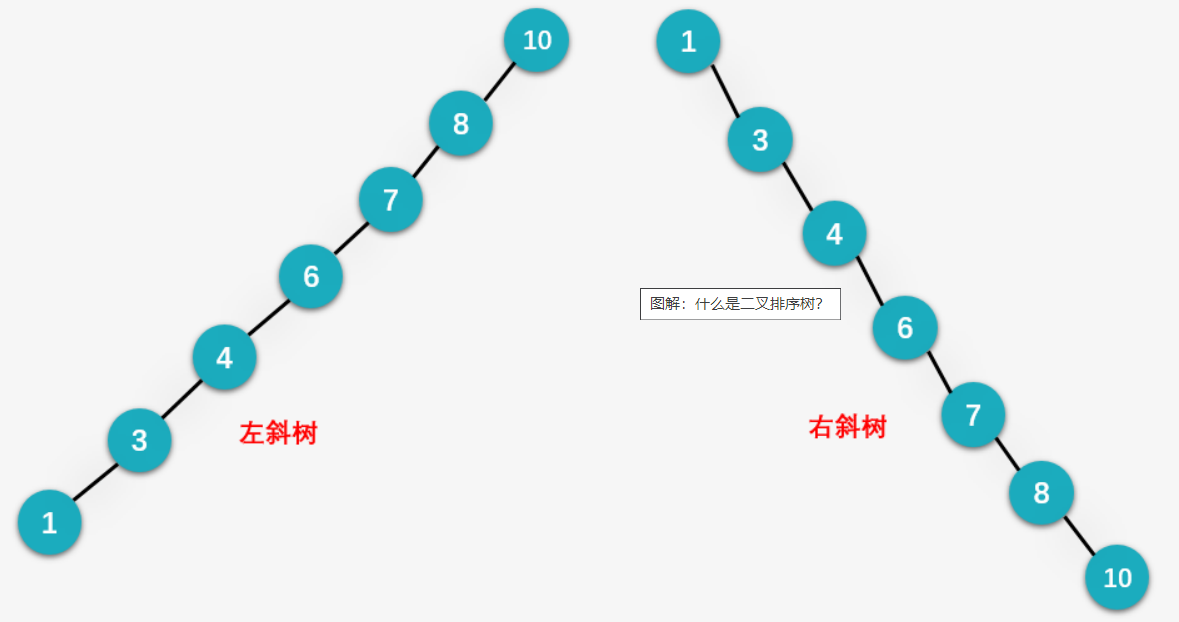
查找复杂度取决于深度，好的话是二叉树的O(logn)，坏的话就是斜树的O(n)

实现

这里采用typescript实现，所以先定义好类型

export class BSTreeNode<T = number> {
  val: T;
  left: BSTree<T>;
  right: BSTree<T>;

  constructor(val: T, left?: BSTree<T>, right?: BSTree<T>) {
    this.val = val;
    this.left = left ? left : null;
    this.right = right ? right : null;
  }
}
export type BSTree<T = number> = BSTreeNode<T> | null;

新增

如果新增节点的值比当前节点大，则插入到节点右边，小则插入到左边

/** 新增节点: 作为叶子节点插入 */
export function insertBSTreeNode<T>(root: BSTree<T>, val: T): BSTree<T> {
  if (root === null) return new BSTreeNode(val);
  if (val < root.val) {
    if (root.left === null) {
      root.left = new BSTreeNode(val);
    } else {
      insertBSTreeNode(root.left, val);
    }
  } else {
    if (root.right === null) {
      root.right = new BSTreeNode(val);
    } else {
      insertBSTreeNode(root.right, val);
    }
  }
  return root;
}

通过数组构建二叉排序树

其实就是遍历数组的值不断新增即可

/** 构建二叉排序树 */
export function createBSTree<T>(arr: T[]): BSTree<T> {
  if (arr.length === 0 || arr[0] === null) return null;
  const root = new BSTreeNode(arr[0]);
  for (let i = 1; i < arr.length; i++) {
    insertBSTreeNode(root, arr[i]);
  }
  return root;
}

遍历二叉排序树

这里通过中序遍历 直接获得一个有序序列

/** 遍历二叉排序树: 中序遍历 */
export function traverseBSTree<T>(root: BSTree<T>): T[] {
  if (root === null) return [];
  const arr: T[] = [];
  const left = traverseBSTree(root.left);
  arr.push(...left, root.val);
  const right = traverseBSTree(root.right);
  return [...arr, ...right];
}

查找节点

其实就是通过判断大小来查找，如果比当前节点大就在右子树查找，否则左子树查找

/** 查找节点 */
export function findBSTressNode<T>(root: BSTree<T>, val: T): BSTree<T> {
  if (root === null) return null;
  if (root.val === val) return root;
  if (val < root.val) return findBSTressNode(root.left, val);
  return findBSTressNode(root.right, val);
}

一些特性方法

前驱后驱的意思是有序序列下的上一个节点和下一个节点，比如上图中8的前驱节点是7，后驱节点是9。

其中获取前后驱节点在删除方法时候需要用到

/** 获取树的最小节点 */
export function getMinBSTreeNode<T>(root: BSTree<T>): BSTree<T> {
  if (root === null) return null;
  if (root.left === null) return root;
  return getMinBSTreeNode(root.left);
}

/** 获取树的最大节点 */
export function getMaxBSTreeNode<T>(root: BSTree<T>): BSTree<T> {
  if (root === null) return null;
  if (root.right === null) return root;
  return getMaxBSTreeNode(root.right);
}

/** 获取前驱节点: 左子节点树的最大值 */
export function getPrevBSTreeNode<T>(root: BSTree<T>): BSTree<T> {
  if (root === null) return null;
  if (root.left === null) return null;
  return getMaxBSTreeNode(root.left);
}

/** 获取后驱节点: 右子节点树的最小值 */
export function getNextBSTressNode<T>(root: BSTree<T>): BSTree<T> {
  if (root === null) return null;
  if (root.right === null) return null;
  return getMinBSTreeNode(root.right);
}

删除节点

这个方法也是所有方法中最复杂的，待删除节点可细分为以下情况

1. 叶子节点: 直接删除
2. 节点只有左子树或者右子树: 节点删除 将节点的左子树或者右子树移到删除节点的位置上
3. 节点既有左子树也有右子树: 找到节点的前驱/后继节点替换该节点 并删除前驱/后继节点(递归删除)

/** 删除节点 **/
export function removeBSTreeNode<T>(root: BSTree<T>, val: T): BSTree<T> {
  if (root === null) return null;
  if (root.val === val) {
    if (root.left === null && root.right === null) {
      // 叶子节点
      return null;
    } else if (root.left === null) {
      // 只存在右子树
      return root.right;
    } else if (root.right === null) {
      // 只存在左子树
      return root.left;
    } else {
      // 既存在左子树也存在右子树 这里采用寻找后继节点替换的方式
      const nextNode = getNextBSTressNode(root)!;
      root.val = nextNode.val; // 将后继节点的值赋值给当前节点
      root.right = removeBSTreeNode(root.right, nextNode.val); // 递归删除后继节点
    }
  } else if (root.val > val) {
    root.left = removeBSTreeNode(root.left, val);
  } else {
    root.right = removeBSTreeNode(root.right, val);
  }
  return root;
}

总结

二叉排序树是一个专门为查找而诞生的树，如果构建得当是可以将查找的效率降低到O(logn)的情况，但是如果构建成斜树的情况，其实和链表就是一样的了，查找复杂度变成O(n)。