平衡二叉树

介绍

定义

平衡二叉树又叫平衡二叉排序树，听名字知道和二叉排序树相关。实际上平衡二叉树就是每个节点最大高度差为1的二叉排序树。

相比较二叉排序树，平衡二叉树查找，插入和删除的时间复杂度都维持在O(logn)。不了解二叉排序树的可以看看我的上一篇文章二叉排序树

平衡因子

节点左右子树的高度差就是平衡因子，值只能为0, -1和1，分别对应左右等高，右比左高，左比右高。叶子节点的平衡因子始终为0

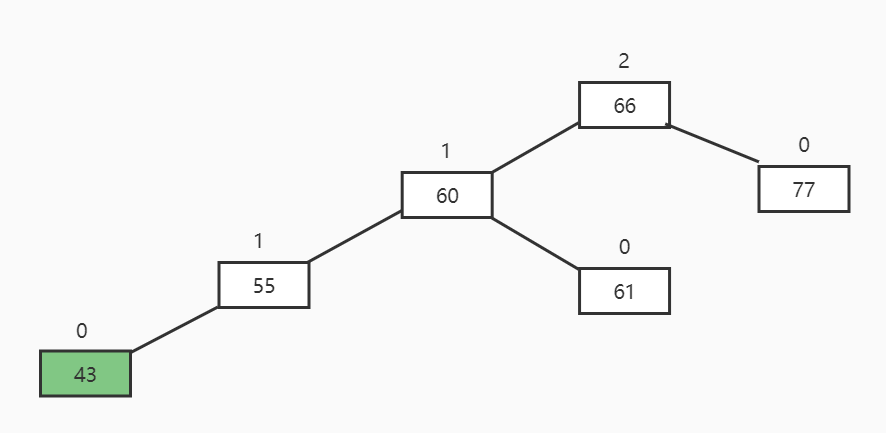
最小失衡树

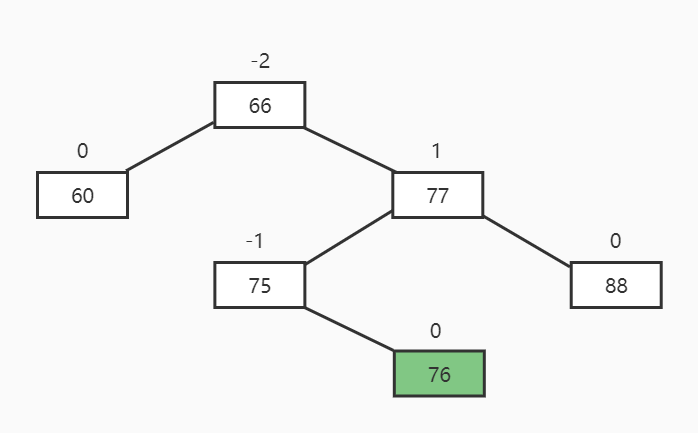
新插入的节点向上查找，第一个平衡因子绝对值超过1的节点为根的子树，比如上图中最小失衡树就是66。

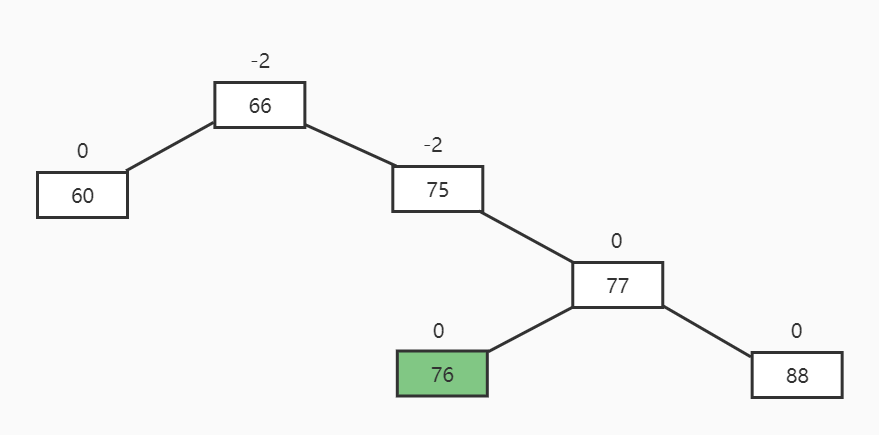
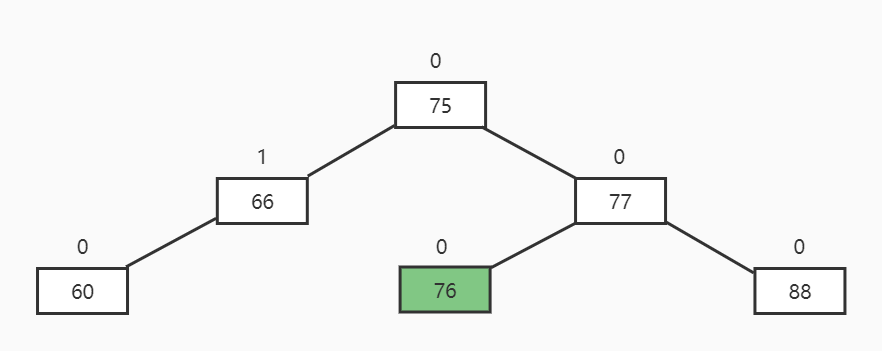
新增和删除节点都会导致树的失衡，失衡调整就是通过旋转最小失衡树来降低高度，旋转方向有左旋和右旋。

失衡调整的四种情况

LL插入

描述: 根节点平衡因子为+2，左节点平衡因子为+1

旋转方向: 右旋

最终结果: 左节点上位

具体操作:

• 根节点的左节点替换根节点位置
• 根节点的左节点的右子树变成根节点的左子树
• 根节点本身变成左节点的右子树

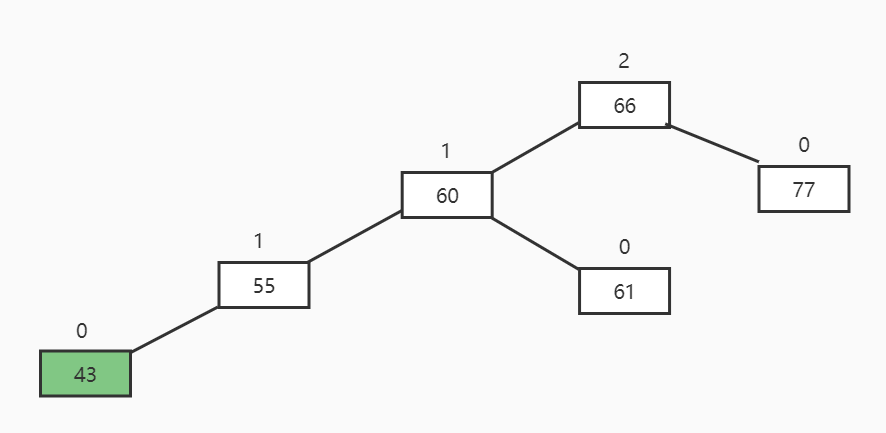
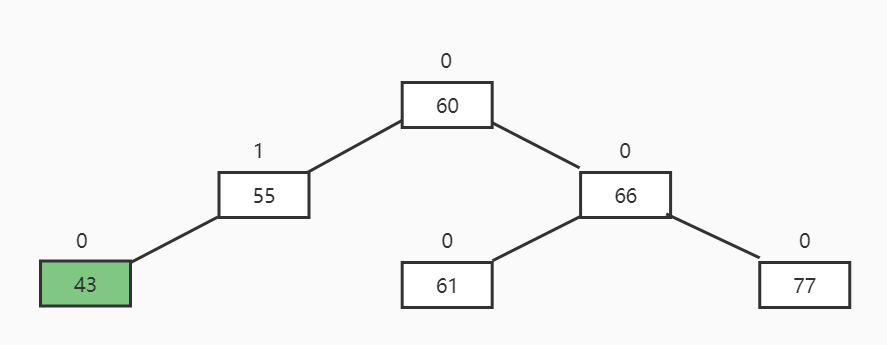
RR插入

描述: 根节点平衡因子为-2，右节点平衡因子为-1

旋转方向: 左旋

最终结果: 右节点上位

具体操作:

• 根节点的右节点替换根节点位置
• 根节点的右节点的左子树变成根节点的右子树
• 根节点本身变成右节点的左子树

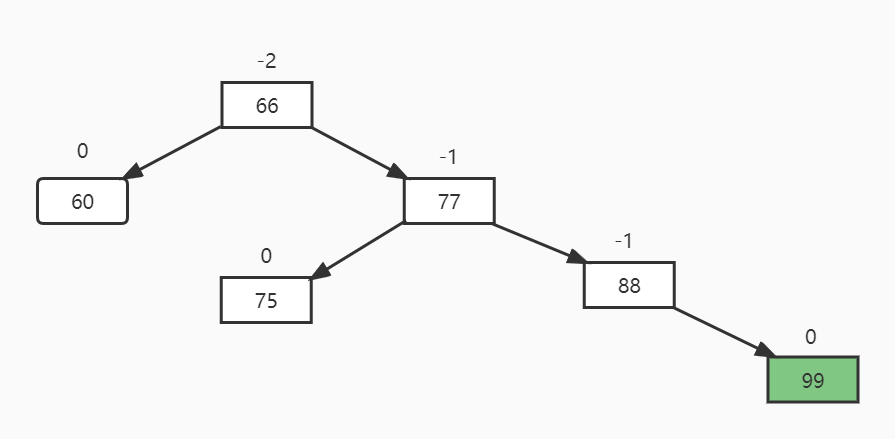
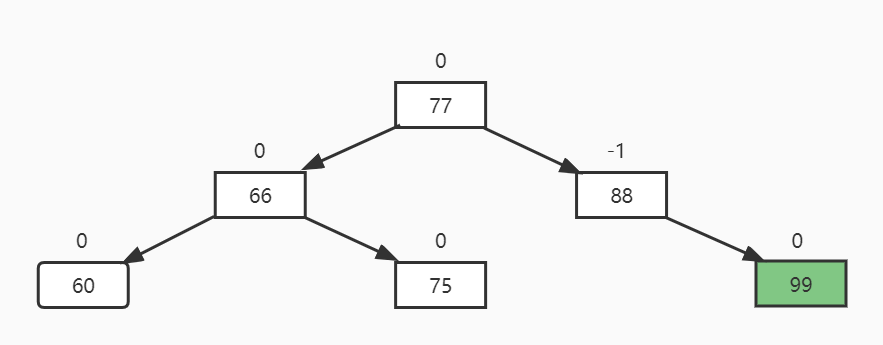
LR插入

描述: 根节点平衡因子为+2，左节点平衡因子为-1

旋转方向: 左节点左旋再根节点右旋

最终结果: 左节点的右节点上位

具体操作:

• 左节点左旋再根节点右旋

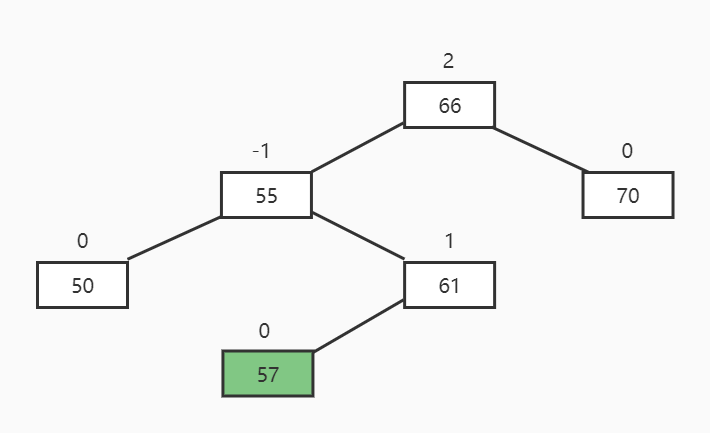
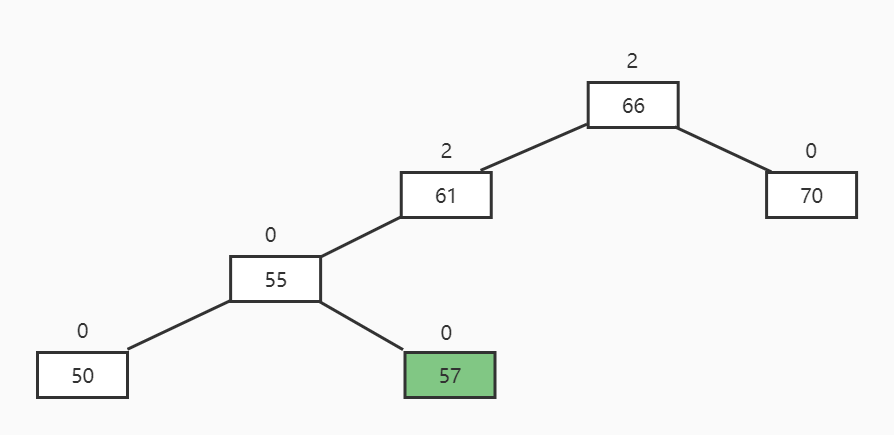
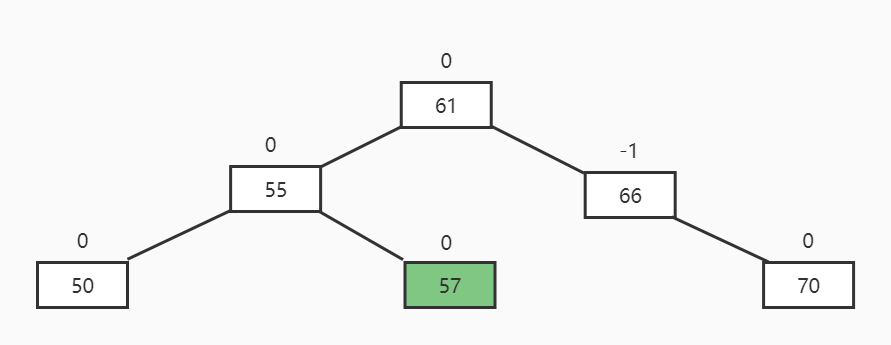
RL插入

描述: 根节点平衡因子为-2，右节点平衡因子为+1

旋转方向: 右节点右旋再根节点左旋

最终结果: 右节点的左节点上位

具体操作:

• 右节点右旋再根节点左旋

实现

因为采用typescript所以先定义好类型，可以看到相比较二叉排序树多了个深度属性，主要是方便计算平衡因子.

 export class AVLTreeNode<T = number> {
  val: T;
  left: AVLTree<T>;
  right: AVLTree<T>;
  depth: number;

  constructor(val: T, left?: AVLTree<T>, right?: AVLTree<T>) {
    this.val = val;
    this.left = left ? left : null;
    this.right = right ? right : null;
    this.depth = 1;
  }
}
export type AVLTree<T = number> = AVLTreeNode<T> | null;

旋转操作

旋转是保证平衡二叉树高度平衡的必要操作，以至于不会出现二叉排序树那种斜树的情况

/** 获取树的深度 */
export function getAVLTreeDepth<T>(root: AVLTree<T>): number {
  if (root === null) return 0;
  return root.depth;
}

/** 更新树的深度 */
export function updateAVLTreeDepth<T>(root: AVLTree<T>) {
  if (root === null) throw new Error("非法节点");
  root.depth = Math.max(getAVLTreeDepth(root.left), getAVLTreeDepth(root.right)) + 1;
}

/** 获取节点的平衡因子 */
export function getAVLTreeNodeBalance<T>(node: AVLTree<T>) {
  if (node === null) throw new Error("非法节点");
  return getAVLTreeDepth(node.left) - getAVLTreeDepth(node.right);
}

/** 左旋 */
export function leftRotate<T>(root: AVLTree<T>) {
  if (root === null) return null;
  // 旋转调整
  const newRoot = root.right!;
  const newRootLeft = newRoot.left;
  root.right = newRootLeft; // 根节点的右节点的左子树变成根节点的右子树
  newRoot.left = root; // 根节点本身变成右节点的左子树
  // 调整新老根节点的深度 newRootLeft深度不会改变无须调整
  updateAVLTreeDepth(root);
  updateAVLTreeDepth(newRoot);
  // 返回新的根节点
  return newRoot;
}

/** 右旋 */
export function rightRotate<T>(root: AVLTree<T>) {
  if (root === null) return null;
  // 旋转调整
  const newRoot = root.left!;
  const newRootRight = newRoot.right;
  root.left = newRootRight; // 根节点的左节点的右子树变成根节点的左子树
  newRoot.right = root; // 根节点本身变成左节点的右子树
  // 调整新老根节点的深度 newRootLeft深度不会改变无须调整
  updateAVLTreeDepth(root);
  updateAVLTreeDepth(newRoot);
  // 返回新的根节点
  return newRoot;
}

/** 保持树平衡 */
export function keepAVLTreeBalance<T>(root: AVLTree<T>) {
  if (root === null) return null;
  // 旋转操作
  const balance = getAVLTreeNodeBalance(root);
  if (balance < -1) {
    if (getAVLTreeNodeBalance(root.right) > 0) {
      root.right = rightRotate(root.right); // 节点右节点平衡因子大于0则右旋
    }
    return leftRotate(root); // 平衡因子小于-1则左旋
  }
  if (balance > 1) {
    if (getAVLTreeNodeBalance(root.left) < 0) {
      root.left = leftRotate(root.left); // 节点左节点平衡因子小于0则左旋
    }
    return rightRotate(root); // 平衡因子大于1则右旋
  }
  return root;
}

新增操作

和二叉排序树几乎一样，唯一区别就是每次新增完节点需要更新下父节点深度，然后对父节点进行一次旋转操作

/** 新增节点 */
export function insertAVLTreeNode<T>(root: AVLTree<T>, val: T): AVLTree<T> {
  if (root === null) return new AVLTreeNode(val);
  if (val < root.val) {
    root.left = insertAVLTreeNode(root.left, val);
  } else {
    root.right = insertAVLTreeNode(root.right, val);
  }
  // 修改节点的深度
  updateAVLTreeDepth(root);
  // 返回平衡后的结果
  return keepAVLTreeBalance(root);
}

构建平衡二叉树

和二叉排序树一样，只不过因为根节点会变，所以需要不断赋新值

export function createAVLTree<T>(arr: T[]): AVLTree<T> {
  if (arr.length === 0 || arr[0] === null) return null;
  let root: AVLTree<T> = new AVLTreeNode(arr[0]);
  for (let i = 1; i < arr.length; i++) {
    root = insertAVLTreeNode(root, arr[i]); // 根节点需要重新赋值
  }
  return root;
}

遍历平衡二叉树

和二叉排序树一样，就是中序遍历获取有序序列

/** 遍历平衡二叉树: 中序遍历 */
export function traverseAVLTree<T>(root: AVLTree<T>): T[] {
  if (root === null) return [];
  const arr: T[] = [];
  const left = traverseAVLTree(root.left);
  arr.push(...left, root.val);
  const right = traverseAVLTree(root.right);
  return [...arr, ...right];
}

查找节点

同二叉排序树，通过比较大小查找

/** 查找节点 */
export function findAVLTressNode<T>(root: AVLTree<T>, val: T): AVLTree<T> {
  if (root === null) return null;
  if (root.val === val) return root;
  if (val < root.val) return findAVLTressNode(root.left, val);
  return findAVLTressNode(root.right, val);
}

删除节点

也是同二叉排序树一样，只不过删除后的父节点多了更新深度和旋转的操作

/** 获取树的最小节点 */
export function getMinAVLTreeNode<T>(root: AVLTree<T>): AVLTree<T> {
  if (root === null) return null;
  if (root.left === null) return root;
  return getMinAVLTreeNode(root.left);
}

/** 获取树的最大节点 */
export function getMaxAVLTreeNode<T>(root: AVLTree<T>): AVLTree<T> {
  if (root === null) return null;
  if (root.right === null) return root;
  return getMaxAVLTreeNode(root.right);
}

/** 获取前驱节点: 左子节点树的最大值 */
export function getPrevAVLTreeNode<T>(root: AVLTree<T>): AVLTree<T> {
  if (root === null) return null;
  if (root.left === null) return null;
  return getMaxAVLTreeNode(root.left);
}

/** 获取后驱节点: 右子节点树的最小值 */
export function getNextAVLTressNode<T>(root: AVLTree<T>): AVLTree<T> {
  if (root === null) return null;
  if (root.right === null) return null;
  return getMinAVLTreeNode(root.right);
}

/** 删除节点
  1. 叶子节点: 直接删除
  2. 节点只有左子树或者右子树: 节点删除 将节点的左子树或者右子树移到删除节点的位置上
  3. 节点既有左子树也有右子树: 找到节点的前驱/后继节点替换该节点 并删除前驱/后继节点(递归删除)

  删除完调整树的平衡
*/
export function removeAVLTreeNode<T>(root: AVLTree<T>, val: T): AVLTree<T> {
  if (root === null) return null;
  if (root.val === val) {
    if (root.left === null && root.right === null) {
      // 叶子节点
      return null;
    } else if (root.left === null) {
      // 只存在右子树
      return root.right;
    } else if (root.right === null) {
      // 只存在左子树
      return root.left;
    } else {
      // 既存在左子树也存在右子树 这里采用寻找后继节点替换的方式
      const nextNode = getNextAVLTressNode(root)!;
      root.val = nextNode.val; // 将后继节点的值赋值给当前节点
      root.right = removeAVLTreeNode(root.right, nextNode.val); // 递归删除后继节点
    }
  } else if (root.val > val) {
    root.left = removeAVLTreeNode(root.left, val);
  } else {
    root.right = removeAVLTreeNode(root.right, val);
  }
  // 修改节点的深度
  updateAVLTreeDepth(root);
  // 返回平衡后的结果
  return keepAVLTreeBalance(root);
}

总结

其实相比较二叉排序树，平衡二叉树就是通过旋转操作让树的深度不会无限递增，将查找复杂度降低到了O(logn)级别。除了新增和删除需要旋转下树外，其他并没有什么区别。