二叉堆

基础

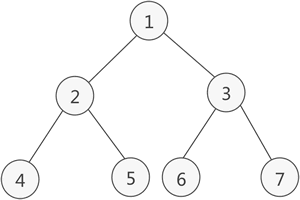
满二叉树

定义: 除最后一层没有任何子节点外 每一层节点都有两个子节点

数学公式: 层次为h(从0开始) 深度为d(h+1) 节点总数n

• 每一层的节点个数: 2^n
• 节点总数: 2^d -1
• 深度: log2n

完全二叉树

定义: 除了最后一层外 其他各层节点数都是满的 且最后一层的节点都连续集中在左边

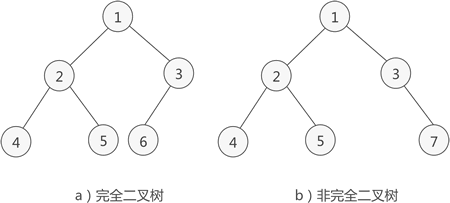
二叉堆

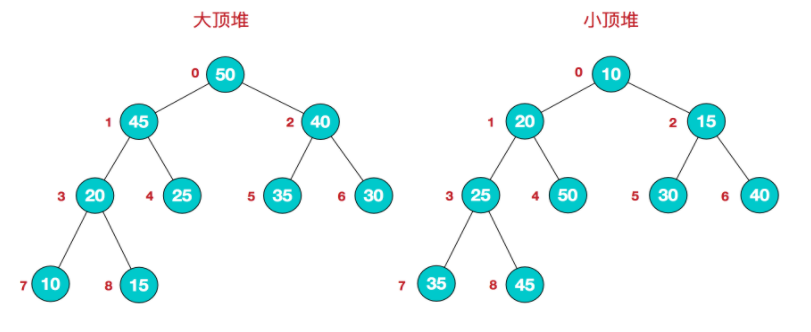
定义: 二叉树就是满足如下性质的完全二叉树

• 大顶堆: 父节点的值比每个子节点的值要大
• 小顶堆: 父节点的值比每个子节点的值要小

特点

• 堆顶永远是最大/最小值 但是其他元素顺序未知

堆操作

• 堆上浮: 将节点和父节点进行比较 如果不满足堆条件则和父节点交换 直到满足条件
• 堆下沉: 将节点和子节点比较 找到最符合堆条件的节点和父节点交换 直到满足条件
• 添加元素: 将节点添加到堆尾，然后执行上浮操作，复杂度O(log2n)
• 弹出元素: 交换堆顶和堆尾元素值，然后弹出堆尾，复杂度O(log2n)
• 获取堆顶元素值: 复杂度O(1)

用途

• 作为优先级队列
• 堆排序 复杂度O(logn)

实现

class Heap {
  protected heapArr: number[];

  constructor() {
    this.heapArr = [0]; // 下标从1开始
  }

  // 交换
  private swap(i: number, j: number) {
    [this.heapArr[j], this.heapArr[i]] = [this.heapArr[i], this.heapArr[j]];
  }
  // 获取左节点索引
  private getLeftIndex(i: number) {
    return 2 * i;
  }
  // 获取右节点索引
  private getRightIndex(i: number) {
    return 2 * i + 1;
  }
  // 获取父节点索引
  private getParentIndex(i: number) {
    return i >> 1;
  }

  // 对比方法-默认小顶堆
  protected compare(parentIndex: number, childIndex: number) {
    return this.heapArr[parentIndex] < this.heapArr[childIndex];
  }
  // 上浮
  private shiftUp(i: number) {
    while (i > 1 && this.compare(this.getParentIndex(i), i) === false) {
      const parentIndex = this.getParentIndex(i);
      this.swap(i, parentIndex); // 交换两者的值
      i = parentIndex;
    }
  }
  // 下沉/堆化
  private shiftDown(i: number) {
    while (this.getLeftIndex(i) <= this.size) {
      let childIndex = this.getLeftIndex(i);
      let rightIndex = this.getRightIndex(i);
      // 小顶堆下 如果右节点的值更小 则交换右节点
      if (rightIndex <= this.size && this.compare(rightIndex, childIndex)) childIndex = rightIndex;
      if (this.compare(i, childIndex)) return; // 如果值满足条件则跳出循环
      this.swap(i, childIndex);
      // 继续下沉
      i = childIndex;
    }
  }

  // 获取堆长度
  get size() {
    return this.heapArr.length - 1;
  }
  // 获取堆顶元素
  peek() {
    return this.heapArr[1];
  }
  // 添加元素
  push(item: number) {
    // 添加元素后上浮
    this.heapArr.push(item);
    this.shiftUp(this.size);
  }
  // 弹出元素
  pop() {
    if (this.size === 0) return undefined;
    this.swap(1, this.size);
    const item = this.heapArr.pop();
    this.shiftDown(1); // 下沉
    return item;
  }
}

// 小顶堆
export class MinHeap extends Heap {
  protected compare(parentIndex: number, childIndex: number) {
    return this.heapArr[parentIndex] < this.heapArr[childIndex];
  }
}

// 大顶堆
export class MaxHeap extends Heap {
  protected compare(parentIndex: number, childIndex: number) {
    return this.heapArr[parentIndex] > this.heapArr[childIndex];
  }
}

相关题

215. 数组中的第K个最大元素

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。
请注意，你需要找的是数组排序后的第 `k` 个最大的元素，而不是第 `k` 个不同的元素。

示例:
输入: [3,2,1,5,6,4], k = 2
输出: 5

解法: 通过维护一个长度为k的小顶堆，当遍历完所有结果，堆顶就是第k大的值

function findKthLargest(nums: number[], k: number): number {
  const heap = new MinHeap();
  for (let num of nums) {
    heap.push(num);
    if (heap.size > k) {
      heap.pop();
    }
  }
  return heap.peek();
}

502. IPO

假设 力扣（LeetCode）即将开始IPO。为了以更高的价格将股票卖给风险投资公司，力扣 希望在 IPO 之前开展一些项目以增加其资本。 由于资源有限，它只能在 IPO之前完成最多 k 个不同的项目。帮助 力扣 设计完成最多 k 个不同项目后得到最大总资本的方式。
给你 n 个项目。对于每个项目 i ，它都有一个纯利润 profits[i] ，和启动该项目需要的最小资本 capital[i] 。
最初，你的资本为 w 。当你完成一个项目时，你将获得纯利润，且利润将被添加到你的总资本中。
总而言之，从给定项目中选择 最多 k 个不同项目的列表，以 最大化最终资本 ，并输出最终可获得的最多资本。
答案保证在 32 位有符号整数范围内。

示例：
输入：k = 2, w = 0, profits = [1,2,3], capital = [0,1,1]
输出：4
解释：
由于你的初始资本为 0，你仅可以从 0 号项目开始。
在完成后，你将获得 1 的利润，你的总资本将变为 1。
此时你可以选择开始 1 号或 2 号项目。
由于你最多可以选择两个项目，所以你需要完成 2 号项目以获得最大的资本。
因此，输出最后最大化的资本，为 0 + 1 + 3 = 4。

解决: 通过维护一个大顶堆来获取最大的收益项目，此外这道题还有一个技巧就是通过先将项目进行排序，然后通过维护进度指针来跳过重复项目添加进堆

function findMaximizedCapital(k: number, w: number, profits: number[], capital: number[]): number {
  // 将项目整合成一个数组
  let projects = capital.map((v, i) => [v, profits[i]]);
  projects = projects.sort((a, b) => a[0] - b[0]); // 按照启动资金排序为了不重复添加已做项目 不然每次都要重新获取一次还会重复
  // 大顶堆存储项目利润
  const maxHeap = new MaxHeap();
  // 添加过的项目索引
  let currProjectIndex = 0;

  // 项目次数
  for (let i = 0; i < k; i++) {
    // 获取满足启动资金的项目
    for (let j = currProjectIndex; j < profits.length; j++) {
      if (projects[j][0] <= w) {
        // 如果满足启动资金则添加到大顶堆 添加索引+1
        maxHeap.push(projects[j][1]);
        currProjectIndex++;
      } else {
        // 否则说明当前资金不足以启动资金 直接跳出循环
        break;
      }
    }

    // 如果有项目做完增加启动资金
    if (maxHeap.size > 0) {
      w += maxHeap.pop()!;
    } else {
      // 没有项目做说明启动资金不够了 直接退出
      return w;
    }
  }

  return w;
}